1.Bubble Sort
It is a simple sorting algorithm that works by repeatedly swapping adjacent elements if they are in the wrong order. It is not very efficient and is only suitable for small lists, but it is easy to understand and implement.
.png) |
| Bubble Sort |
How Bubble Sort Work
• Start at the beginning of the list.
• Compare the first two elements. If the first element is greater than the second element, swap them.
• Move to the next pair of elements, and repeat step 2. Continue until you reach the end of the list.
• At this point, the largest element is at the end of the list.
• Repeat the above steps for all the elements except for the last one.
• Continue this process until the entire list is sorted.
Example:-
Given the list [5, 2, 8, 3, 1], we start at the beginning and compare the first two elements:
Since 5 is greater than 2, we swap them:
We move to the next pair of elements and compare them:
Since 8 is greater than 3, we swap them:
We move to the next pair of elements and compare them:
Since 8 is greater than 1, we swap them:
At this point, we've reached the end of the list, so the largest element (8) is in its correct position. We repeat the above steps for the remaining elements until the entire list is sorted:
[2, 5, 3, 1, 8] -> [2, 3, 5, 1, 8] -> [2, 3, 1, 5, 8] -> [2, 1, 3, 5, 8] -> [1, 2, 3, 5, 8]
The final result is a sorted list: [1, 2, 3, 5, 8].
2. Insertion Sort
It is a sorting algorithm that builds the final sorted array one item at a time. It is efficient for small lists and is used as part of more complex algorithms. The basic idea behind insertion sort is to divide the input array into two sub-arrays: a sorted sub-array and an unsorted sub-array. Initially, the sorted sub-array is empty, and the unsorted sub-array is the entire input array. The algorithm then proceeds to insert each element of the unsorted sub-array into its correct position in the sorted sub-array.
How Insertion Sort work with example implementation-
.png) |
| Insertion Sort |
We will use the insertion sort algorithm to sort this array in ascending order.
Start with the second element of the array (i.e., index 1), which is 2, and compare it with the first element (i.e., index 0), which is 7. Since 2 is smaller than 7, swap them.
Consider the third element (i.e., index 2), which is 4. Compare it with the second element (i.e., index 1), which is 7, and insert it into its correct position among the first three elements.
Consider the fourth element (i.e., index 3), which is 1. Compare it with the third element (i.e., index 2), which is 7, and move the third element to the right. Then, compare the fourth element with the second element (i.e., index 1), which is 4, and move the second element to the right. Finally, insert the fourth element into its correct position among the first four elements.
Consider the fifth element (i.e., index 4), which is 5. Compare it with the fourth element (i.e., index 3), which is 7, and insert it into its correct position among the first five elements.
Consider the sixth element (i.e., index 5), which is 3. Compare it with the fifth element (i.e., index 4), which is 7, and move the fifth element to the right. Then, compare the sixth element with the fourth element (i.e., index 3), which is 5, and move the fourth element to the right. Finally, compare the sixth element with the third element (i.e., index 2), which is 4, and move the third element to the right. Insert the sixth element into its correct position among the first six elements.
The array is now fully sorted.
And there you have it! The insertion sort algorithm has sorted the array in ascending order.
Selection sort
It is a simple sorting algorithm that works by repeatedly finding the minimum element from an unsorted array and putting it at the beginning of the array. This process is repeated for the remaining unsorted part of the array until the entire array is sorted.
How the selection sort algorithm works with Ex-[4, 2, 5, 1, 3]
1.First, the algorithm initializes a "sorted" portion of the array, which initially contains no elements, and an "unsorted" portion of the array, which contains all the elements of the original array.
First iteration: The smallest element in the array [4, 2, 5, 1, 3] is 1, which is at index 3. Swap the first element (4) with the smallest element (1), resulting in the array [1, 2, 5, 4, 3].
2.In each iteration of the algorithm, it finds the smallest element in the unsorted portion of the array and swaps it with the first element of the unsorted portion of the array, which is also the first element of the sorted portion of the array.
Second iteration: The smallest element in the unsorted part of the array [2, 5, 4, 3] is 2, which is at index 1. Swap the second element (2) with the first element of the unsorted part of the array (2), resulting in the array [1, 2, 5, 4, 3].
3.After each iteration, the sorted portion of the array is increased by one element, and the unsorted portion of the array is decreased by one element, since the smallest element has been moved to its correct position in the sorted portion of the array.
Third iteration: The smallest element in the unsorted part of the array [5, 4, 3] is 3, which is at index 4. Swap the third element (5) with the smallest element (3), resulting in the array [1, 2, 3, 4, 5].
4.The algorithm repeats steps 2 and 3 until the entire array is sorted.
Fourth iteration: The smallest element in the unsorted part of the array [4, 5] is 4, which is at index 3. Swap the fourth element (4) with the first element of the unsorted part of the array (4), resulting in the array [1, 2, 3, 4, 5].
Fifth iteration: The smallest (and only) element in the unsorted part of the array [5] is 5, which is already in its correct position. The array remains [1, 2, 3, 4, 5].
At the end of the process, the array is sorted in ascending order.
Merge sort
It is a sorting algorithm that works by dividing an array into two halves, sorting the two halves, and then merging the sorted halves back together. The key idea behind merge sort is that it's easier to sort two smaller sorted arrays and then merge them together, rather than sorting one large unsorted array.
How the merge sort algorithm works with Ex-[4, 2, 5, 1, 3]
1.Divide the unsorted array into two halves, by finding the middle index of the array.
First step: The unsorted array [4, 2, 5, 1, 3] is divided into two halves: [4, 2, 5] and [1, 3].
2.Recursively sort the left half of the array, by calling the merge sort algorithm on the left half.
Second step: The left half [4, 2, 5] is recursively sorted by calling the merge sort algorithm on it, which divides it into [4, 2] and [5], then sorts those into [2, 4] and [5], and finally merges them into [2, 4, 5].
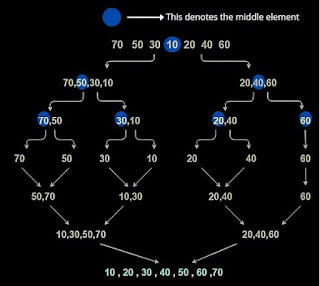.jpeg) |
| Merge sort |
3.Recursively sort the right half of the array, by calling the merge sort algorithm on the right half.
Third step: The right half [1, 3] is recursively sorted by calling the merge sort algorithm on it, which divides it into [1] and [3], then sorts those into [1] and [3], and finally merges them into [1, 3].
4.Merge the sorted left and right halves back together. To do this, create a new temporary array and iterate through both the left and right halves of the array, selecting the smallest element between the two halves and adding it to the temporary array. Once one of the halves has been fully added to the temporary array, simply add the remaining elements of the other half to the temporary array.
Fourth step: The fully sorted left and right halves ([2, 4, 5] and [1, 3]) are merged together by selecting the smallest element between the two halves and adding it to the temporary array. The first element of the left half ([2]) is smaller than the first element of the right half ([1]), so 2 is added to the temporary array. The second element of the left half ([4]) is still smaller than the first element of the right half ([1]), so 4 is added to the temporary array. The third element of the left half ([5]) is larger than the first element of the right half ([1]), so 1 is added to the temporary array. The first element of the right half has now been added to the temporary array, so the remaining elements of the right half ([3]) are added to the temporary array. The fully merged and sorted array is now [1, 2, 3, 4, 5].
5.Return the fully merged and sorted array.
Fifth step: The fully merged and sorted array [1, 2, 3, 4, 5] is returned.
At the end of the process, the array is sorted in ascending order.
NOTE: In upcoming blog we discussed the Quick sort,Heap sort and the types of Searching Algorithms - linear search, binary search, interpolation search, and exponential search.
.png)
.png)
.jpeg)
.jpeg)


.jpeg)


.jpeg)
.jpeg)

0 Comments